5.5. Distorted Phase Effect¶

5.5.1. The Phenomenon¶

Notes for distorted phase effect, ref to [Kneller2015]

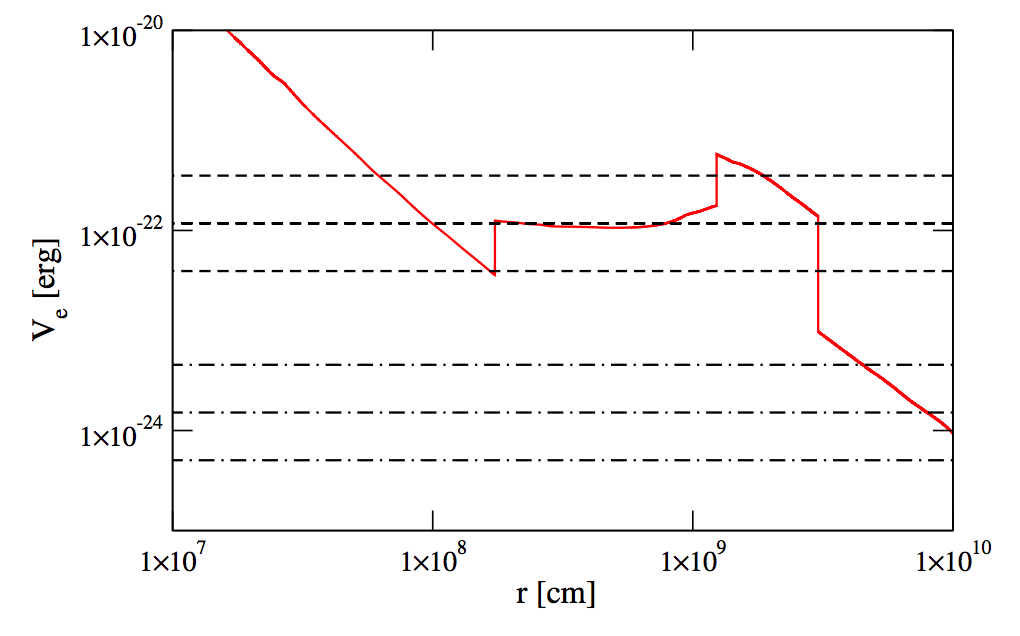
Fig. 5.40 MSW potential for different radius. Multiple breaks appear. [Kneller2015]. The dashed line are the resonance potential requirement for 5MeV, 15MeV, 45MeV neutrino of different mixing parameters \(\delta m^2=2.32\times 10^{-3}\mathrm{eV}^2\), \(\theta=9^{\circ}\) (dashed grid lines) and \(\delta m^2=2.32\times 10^{-3}\mathrm{eV}^2\), \(\theta=33.9^\circ\) (dot-dashed grid lines).¶

Kneller et al calculated the corresponding neutrino transitions.

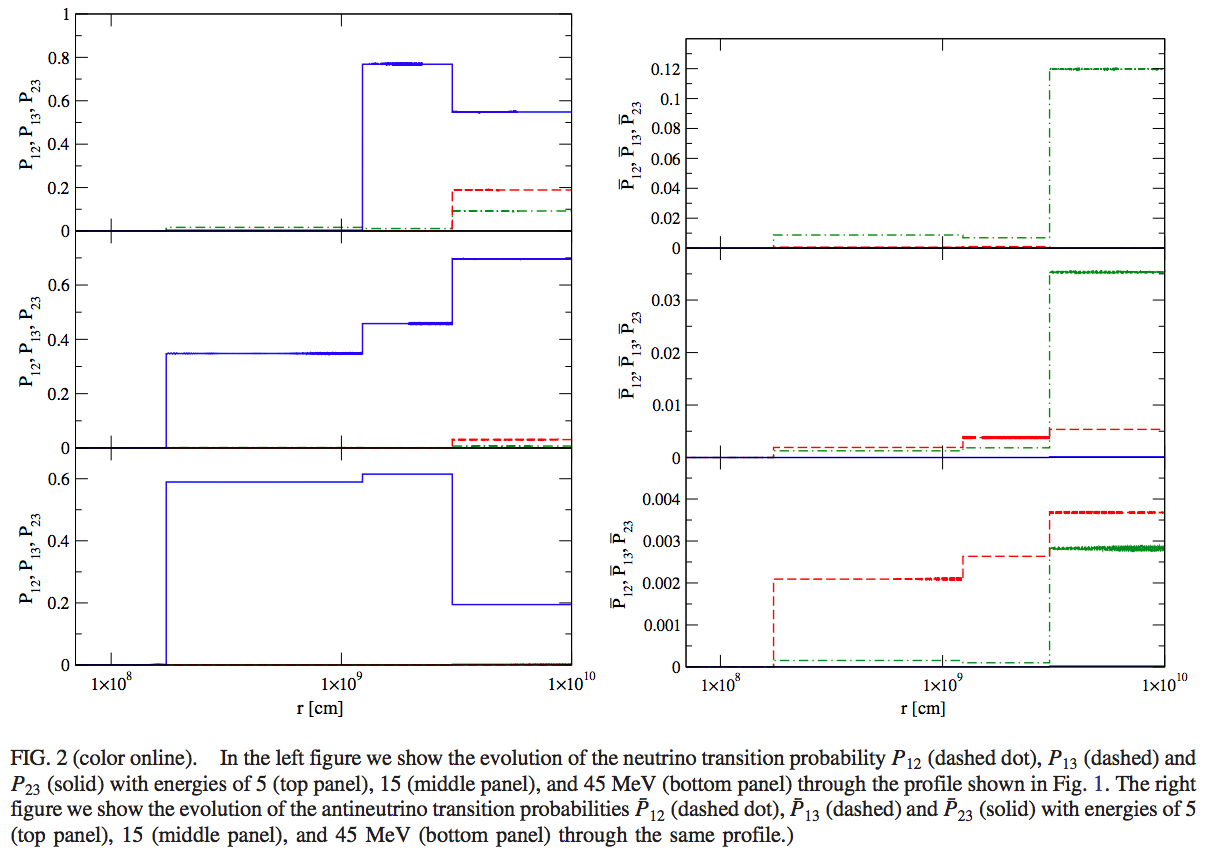
Fig. 5.41 Neutrino transition probabilities through the profile above [Kneller2015]. The first jump for 5MeV neutrinos is due to the density profile break at around \(10^{9}\mathrm{cm}\), while the second jump is due to the profile decrease at around \(5\times 10^{9}\mathrm{cm}\) .¶

I don’t quite understand the drop in probability for 5MeV neutrinos. Is that not simply a constant matter effect?

5.5.2. Refs & Notes¶

Kneller2015(1,2,3): Kneller, J. P., & Kabadi, N. V. (2015). Sensitivity of neutrinos to the supernova turbulence power spectrum: Point source statistics. Physical Review D - Particles, Fields, Gravitation and Cosmology, 92(1), 1–19.
Kneller2017: Kneller, J. P., & Reyes, M. de los. (2017). The effect upon neutrinos of core-collapse supernova accretion phase turbulence. arXiv:1702.06951