1.1. Common Sense¶

1.1.1. Units¶

Natural units makes the calculation of neutrinos convenient. The consequences are

The energy-mass-momentum relations becomes \(E^2 = p^2 + m^2\). Thus mass \(m\), momentum \(\mathbf p\) and energy \(E\) have the same units.
Angular momentum in quantum mechanics is \(L_z = m\hbar\) where \(m\) is a number. \(\hbar\) is of unit angular momentum.
A plane wave in quantum mechanics is \(\Psi = A e^{ \frac{E t - p x}{\hbar} }\). \(\frac{E t - p x}{\hbar}\) should be unitless, which means \(px\) has unit angular momentum, which is obvious, while \(E t\) also has the unit of angular momentum. Previously we noticed momentum has the same unit with energy, we should have time \(t\) has the same unit as length \(x\). Also we can conclude that length and time has the unit of \(1/E\).

One should notice that charge is unit 1 in natural units since

\[F = \frac{Qq}{4\pi r^2}.\]

The conversion between natural units and SI can be down by using the following relations.

\[\begin{split}1 \mathrm{GeV} &= 5.08 \times 10^{15} \mathrm {m^{-1}} \\ 1 \mathrm{GeV} &= 1.8\times 10^{-27} \mathrm{kg}\end{split}\]

1.1.2. Useful Conversions in Neutrino Physics¶

Using natural units, length = time = 1/energy, thus we could scale quantities using energy, or whatever convinient energy or length scale we have.

In vacuum oscillations, the energy scale is the oscillation frequency \(\omega_{v,21}\). The length can be scaled using this energy scale. However, it is only convinient when we can restore the actually length in SI units. To fulfill it, we write down the conversion here. For two flavor oscillation, oscillation angular frequency is given by

\[\omega_{v,21} = \frac{\delta m^2}{2E} = \frac{7.5\times 10^{-5}\mathrm{eV}^2}{2\times 1\mathrm{MeV}} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E} = 3.75\times 10^{-11}\mathrm{eV} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E} .\]

On the other hand, electro-volt is related to length through the useful formula

\[197\mathrm{MeV}\cdot \mathrm{fm} = \hbar c = 1.\]

Thus we have the oscillation angular frequency written as

(1.1)¶\[\begin{split}\omega_{v,21} &= 3.75\times 10^{-11}\mathrm{eV} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E} \\ &= 3.75\times 10^{-17}\mathrm{MeV} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E} \\ &= 1.90\times 10^{-4} \mathrm{m}^{-1} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E}.\end{split}\]

Similarly for \(\Delta m_{32}=2.4\times 10^{-3}\mathrm{eV^2}\) the frequency is

\[\omega_{v,32} =\frac{\Delta m^2_{32}}{2E} = 6.3\times 10^{-3} \mathrm{m}^{-1} \frac{\Delta m^2_{32}}{2.5\times 10^{-3} \mathrm{eV}^2 } \frac{1MeV}{E}.\]

Vacuum oscillation equation of motion is

\[i\frac{d}{d x} \Psi = \frac{\omega_v}{2}(-\cos 2\theta_v \boldsymbol{\sigma_3} + \sin 2\theta_v \boldsymbol{\sigma_1}) \Psi,\]

which can be scaled using the energy scale

\[i\frac{d}{d \hat x} \Psi = \frac{1}{2}(-\cos 2\theta_v \boldsymbol{\sigma_3} + \sin 2\theta_v \boldsymbol{\sigma_1})\Psi ,\]

where \(\hat x = \omega_v x\). This could be convinient for numerical calculations, which, however, requires the relation

\[x = \frac{\hat x}{\omega_v} = \frac{\hat x}{ 1.90\times 10^{-4} \mathrm{m}^{-1} \frac{\delta m^2}{7.5\times 10^{-5}\mathrm{eV}^2} \frac{1\mathrm{MeV}}{E} } = \frac{\hat x}{0.190} \mathrm{km} \frac{7.5\times 10^{-5}\mathrm{eV}^2}{\delta m^2} \frac{E}{1\mathrm{MeV}}.\]

Another important situation is the 2 flavor neutrino oscillation in constant matter background \(\lambda_c = \sqrt{2}G_F n_e\). The energy scale is \(\omega_m\) which is calculated using

(1.2)¶\[\omega_m = \omega_v \sqrt{ \frac{\lambda_c}{\omega_v}^2 + 1 - 2 \frac{\lambda_c}{\omega_v}\cos 2\theta_v }.\]

Meanwhile, the effective mixing angle \(\theta_m\) is determined by

\[\tan 2\theta_m = \frac{\sin 2\theta_v}{\cos 2\theta_v - \frac{\lambda}{\omega_v} }.\]

As we would like to scale the equation of motion like what we did for vacuum equation of motion, i.e.,

\[i \frac{d}{d\hat x} \Psi = \frac{1}{2}(-\cos 2\theta_m \boldsymbol{\sigma_3} + \sin 2\theta_m \boldsymbol{\sigma_1})\Psi ,\]

we find out the scaled distance

\[\hat x = \omega_m x.\]

To reverse the process and find out the actual SI unit distance after the numerical calculation, we use

(1.3)¶\[x = \frac{\hat x}{\omega_m}.\]

The procedure will be the following.

Calculate \(\omega_v\) using (1.1).
Calculate \(\hat\lambda_c = \frac{\lambda_c}{\omega_v}\).
Calculate \(\omega_m\) using (1.2).
Find out the actual distance using (1.3).

1.1.3. Diagrams¶

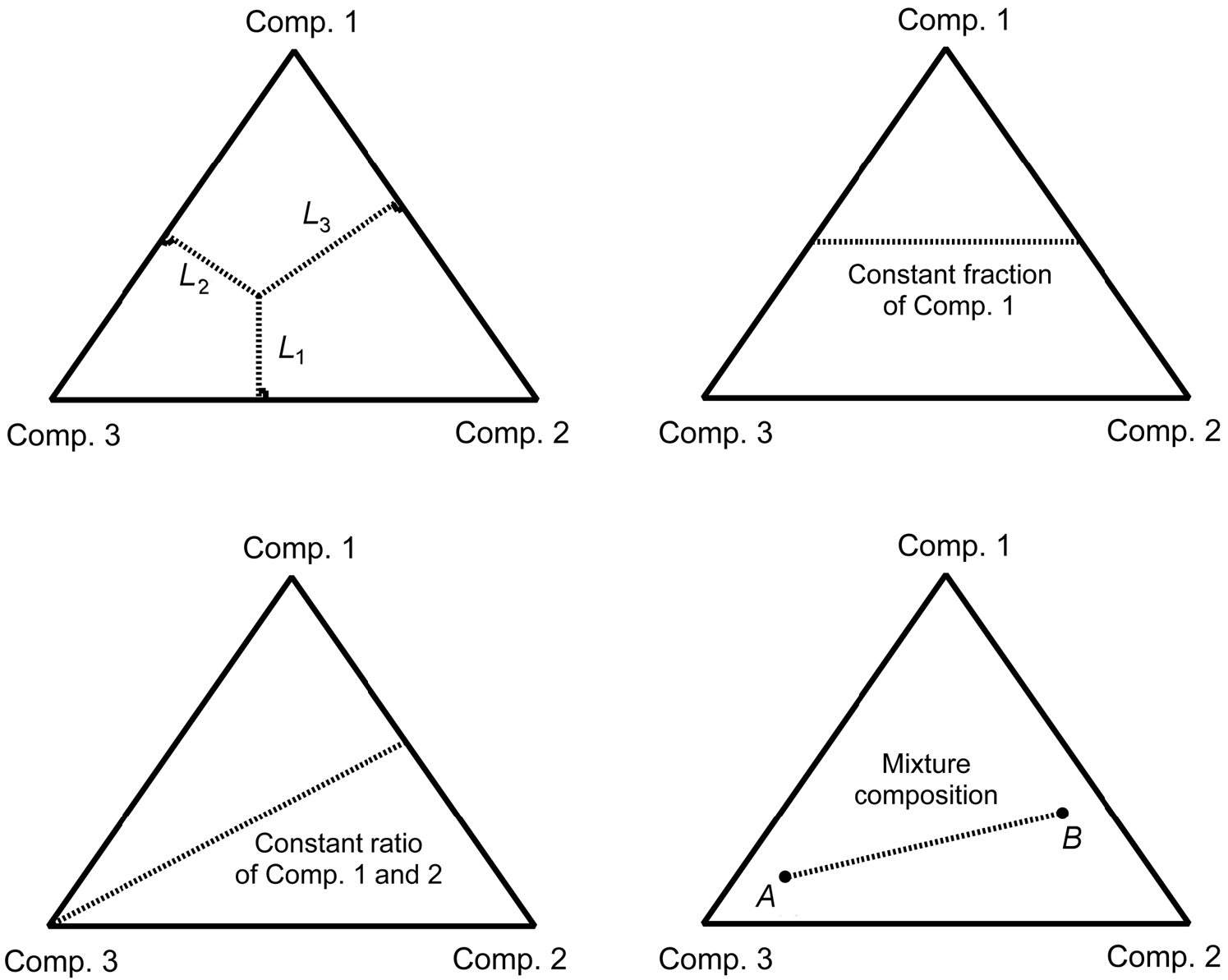
../_images/understandingTernaryDiagram.png — Fig. 1.1 The meanings of points and lines in a ternary diagram. From File:Vol1 Page 380 Image 0001.png@PetroWiki¶

In this documentation on neutrinos, we have all the readings of a point by looking into the line that goes to the left, which means that for the bottom axis, the left is 0 while the right is 1.

1.1.4. Refs and Notes¶

A article about ternary diagram .